Latest Post
Optimization: Newton Raphson Method
- Get link
- X
- Other Apps
Newton Raphson Method Algorithm in C
#include<stdio.h>#include<conio.h>
#include<math.h>
#include<stdlib.h>
float myFun(float x);
int main()
{
float e = 0.01,a,aw = 0,bw = 1,Lw,b,x1,x2,fxa,fxb,fxz,z,j=0;
int i=1,k;
float x[100],dx[100],fdx[100],fddx[100];
x[1] = 1;
dx[1] = (x[i]*1)/100;
begin:
if(j<100)
{
dx[i] = (x[i]*1)/100;
fdx[i] = ((myFun(x[i] + dx[i])) - (myFun(x[i] - dx[i])))/(2*dx[i]);
fddx[i] = ((myFun(x[i] + dx[i])) - (2*myFun(x[i])) + (myFun(x[i] - dx[i])))/(dx[i]*dx[i]);
printf("\nf'(%d) = %.4f",i,fdx[i]);
printf("\nf''(%d) = %.4f",i,fddx[i]);
k = i+1;
x[k] = (x[i] - (fdx[i] / fddx[i]));
printf("\n\nf(%d) = %.4f",k,x[k]);
dx[k] = (x[k]*1)/100;
fdx[k] = ((myFun(x[k] + dx[k])) - (myFun(x[k] - dx[k])))/(2*dx[k]);
if (fdx[k] < 0)
{
fdx[k] = ((-1)*fdx[k]);
}
if (fdx[k] > e)
{
j = j + 1;
i = i + 1;
goto begin;
}
else
{
printf("\n\nf'(%d) = %.9f is Less than termination factor e = %.3f",k,fdx[k],e);
goto end;
}
}
end:
return 0;
}
float myFun(float x) {
float y;
y = ((x*x)+(54/x));
return y; // return statement
}
Output:
 |
| Newton Raphson Method |
- Get link
- X
- Other Apps
Popular posts from this blog
Verilog: 8 to 1 Multiplexer (8-1 MUX) Dataflow Modelling with Testbench Code
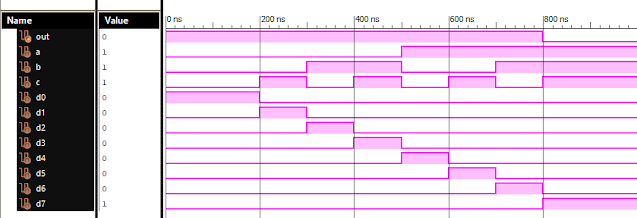
Verilog Code for 8 to 1 Multiplexer Dataflow Modelling module mux_8to1( input a, input b, input c, input D0, input D1, input D2, input D3, input D4, input D5, input D6, input D7, output out, ); module m81( output out, input D0, D1, D2, D3, D4, D5, D6, D7, S0, S1, S2); assign S1bar=~S1; assign S0bar=~S0; assign S2bar=~S2; assign out = (D0 & S2bar & S1bar & S0bar) | (D1 & S2bar & S1bar & S0) | (D2 & S2bar & S1 & S0bar) + (D3 & S2bar & S1 & S0) + (D4 & S2 & S1bar & S0bar) + (D5 & S2 & S1bar & S0) + (D6 & S2 & S1 & S0bar) + (D7 & S2 & S1 & S0); endmodule //Testbench code for 8-1 MUX Dataflow Modelling initial begin // Initialize Inputs a= 0;b = 0;c = 0;D0 = 1;D1 = 0;D2 = 0;D3 = 0;D4 = 0;D5 = 0;D6 = 0;D7 = 0; // Wait 100 ns for global reset to finish #100; // Add stimulus here #100; a = 0;b = 0;c = 1;d0 = ...
VLSI: 8-3 Encoder Dataflow Modelling with Testbench
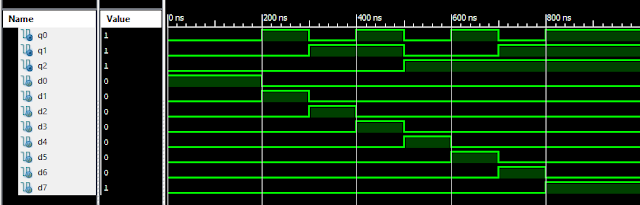
Verilog Code for 8-3 Encoder Dataflow Modelling module encoder_8_to_3( input d0, input d1, input d2, input d3, input d4, input d5, input d6, input d7, output q0, output q1, output q2 ); assign q0 = ( d1 | d3 | d5 | d7 ); assign q1 = ( d2 | d3 | d6 | d7 ); assign q2 = ( d4 | d6 | d5 | d7 ); endmodule //Testbench code for 8-3 Encoder Dataflow Modelling initial begin ...
VLSI: 1-4 DEMUX (Demultiplexer) Dataflow Modelling with Testbench
Verilog Code for 1-4 DEMUX Dataflow Modelling module demux_1_to_4( input d, input s0, input s1, output y0, output y1, output y2, output y3 ); assign s1n = ~ s1; assign s0n = ~ s0; assign y0 = d& s0n & s1n; assign y1 = d & s0 & s1n; assign y2 = d & s0n & s1; assign y3 = d & s0 & s1; endmodule //Testbench code for 1-4 DEMUX Dataflow Modelling initial begin // Initialize Inputs ...
Verilog: 2 - 4 Decoder Structural/Gate Level Modelling with Testbench
Verilog Code for 2-4 Decoder Structural/Gate Level Modelling 2-4 Line Decoder module decoder_2_to_4( input a0, input a1, output d0, output d1, output d2, output d3 ); not (an0,a0),(an1,a1); and (d0,an0,an1),(d1,a0,an1),(d2,an0,a1),(d3,a0,a1); endmodule //Testbench code for 2-4 Decoder Structural/Gate Level Modelling initial begin // Initialize Inputs a0 = 0;a1 = 0; // Wait 100 ns for global reset to finish #100; // Add stimulus here #100; a0=1;a1=0; #100; a0=0;a1=1; #100; a0=1;a1=1; end Output: Verilog 2-4 Decoder Response Other Verilog Programs: Go to Index of Verilog Prog...
Verilog: 1to 8 DeMultiplexer (1-8 DEMUX) Dataflow Modelling with Testbench Code
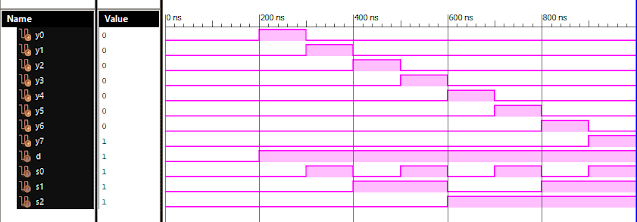
Verilog Code for 1 to 8 DeMultiplexer Dataflow Modelling module demux_1_to_8( input d, input s0, input s1, input s2, output y0, output y1, output y2, output y3, output y4, output y5, output y6, output y7 ); assign s0n = ~ s0; assign s1n = ~ s1; assign s2n = ~ s2; assign y0 = d & s0n & s1n & s2n; assign y1 = d & s0 & s1n & s2n; assign y2 = d & s0n & s1 & s2n; assign y3 = d & s0 & s1 & s2n; assign y4 = d & s0n & s1n & s2; assign y5 = d & s0 & s1n & s2; assign y6 = d & s0n & s1 & s2; assign y7 = d & s0 & s1 & s2; endmodule //Testbench code for 1-8 DEMUX Dataflow Modelling initial begin // Initialize Inputs d = 0;s0 = 0;s1 = 0;s2 = 0; // Wait 100 ns for global reset to finish #100; // Add stimulus here #100; d = 1;s0 = 0;s1 = 0;s2 = 0; #100; d = 1;s0 = 1;s1 = 0;s2 = 0; #100; d = 1;s0 = 0;s1 = 1;s2 = 0; #100; d = 1;s0 = 1;s1 = 1;s2 = 0; #100; d = 1;s0 = 0;s1 = 0;s2 = 1; ...


Comments
Post a Comment